歩容生成の研究
動物の四足歩行における各脚の協調動作は自然現象の解明，
多脚ロボットへの応用などの観点から興味深い研究対象となっています．
歩容生成に向けた微分方程式を用いた数理モデルとしてリミットサイクルをもつ結合振動子があります．
結合振動子における各振動子の周期軌道を脚のリズムに結び付けて歩容のモデルとするとき，
それらの間に存在する位相差が重要となります．
スチュアート・ランダウ方程式
この研究ではリミットサイクルをもつ振動子としてスチュアート・ランダウ方程式を採用しています．
それは複素数 $z(t)$ を用いたつぎの微分方程式です．
\[
\dot{z}(t) = (\mu+ \omega i)z(t)-(1+bi)|z(t)|^2z(t)
\]
ただし，$\mu$, $\omega$，$b$ は実数の定数，
$i$ は虚数単位です．
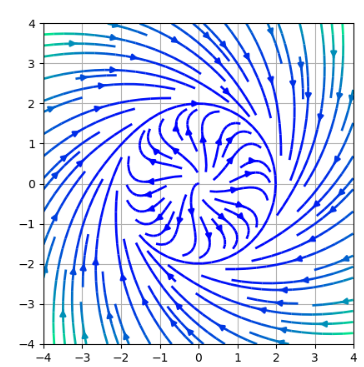
複素平面上の任意の点を初期値 $z(0)$ としたとき，解 $z(t)$ の軌道は
半径 $\sqrt{\mu}$，角速度 $\omega-b\mu$ の円軌道にリミットサイクルとして収束します．
結合振動子
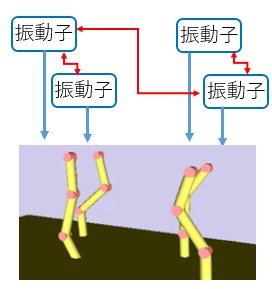
複素数 $z_i(t)$ $(i=1, \cdots, n)$ を
変数とする $n$ 個のスチュアート・ランダウ方程式の周期解の位相を各脚の往復運動に
対応づけます．
脚間には相互作用が存在するとし，それらを結合項として加えたつぎの結合振動子をこの研究における
歩容生成のモデルとします．
\[
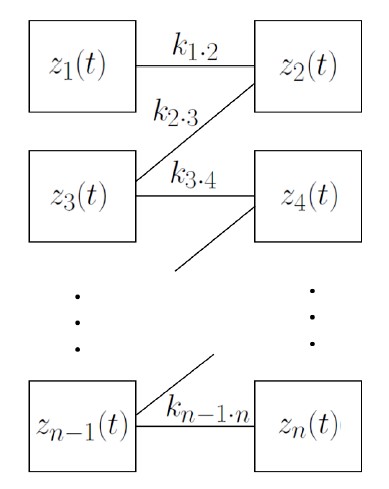\dot{z}_1(t) = (\mu_1 + \omega_1 i) z_1(t) - (1+b_1i)|z_1(t)|^2z_1(t) + k_{1\cdot2}(z_2(t)-z_1(t))
\]
\[
\dot{z}_2(t) = (\mu_2 + \omega_2 i) z_2(t) - (1+b_2i)|z_2(t)|^2z_2(t) + k_{1\cdot2}(z_1(t)-z_2(t))
+ k_{2\cdot3}(z_3(t)-z_2(t))
\]
\[
\vdots
\]
\[ \dot{z}_{n-1}(t) = (\mu_{n-1} + \omega_{n-1}i) z_{n-1}(t) - (1+b_{n-1}i)|z_{n-1}(t)|^2z_{n-1}(t)
+ k_{n-2\cdot n-1}(z_{n-2}(t)-z_{n-1}(t))
+ k_{n-1\cdot n}(z_n(t)-z_{n-1}(t))
\]
\[
\dot{z}_n(t) = (\mu_n + \omega_n i) z_n(t) - (1+b_ni)|z_n(t)|^2z_n(t) + k_{n-1\cdot n}(z_{n-1}(t)-z_n(t))
\]
ここで，$\mu_i > 0$, $\omega_i$, $b_i$ $(i=1, \cdots, n)$ は実数の定数です．
また，$k_{1\cdot2}$, $k_{2\cdot3}$, $k_{3\cdot4}$, $\cdots$, $k_{n-1\cdot n}$ は振動子間の
結合係数の意味をもつ
実数の定数で，
\[
k_{i\cdot i+1} \neq 0, \ \ i=1, \cdots, n-1
\]
を仮定します．
$z_1$ を左最前列の足，$z_2$ を右最前列の足，$\cdots$,
$z_{n-1}$ を左最後列の足，$z_n$ を右最後列の足に対応づけます．
問題設定
結合振動子には $\mu_i$, $\omega_i$, $b_i$ $k_{1\cdot i}$ $(i=1, \cdots, n)$ というパラメータが存在しています．
簡単化のため $\mu_i=1$, $b_i=0$ とします．
研究で考える問題は，歩行に適した位相差が与えられたとき，パラメータ
$\omega_i$ $(i=1, \cdots, n)$ と $k_{i\cdot i+1}$ $(i=1, \cdots, n-1)$
をいかに設定すべきかを明らかにすることです．
$\omega_i$ は個々の振動子の固有振動数， $k_{i\cdot i+1}$ は振動子間の結合係数であり，
これらの値によって各振動子の挙動が変化し，位相差も影響を受けます．
英語版