Research on Gait Generation
The cooperative movements of quadrupedal walking in animals are interesting research subjects
from the point of view of explanation of natural phenomena and application to multi-legged robots.
We consider a mathematical model via differential equations toward gait generation, which is known as
coupled oscillators with limit cycles. Phase diffrences between the cycles are important factors in the case where
the oscillators are related to the rhythm of the movements of the legs.
Stuart-Randau Equation
In this study, the Stuart-Randau Equation is adopted
for the oscillator with a limit cycle.
It is described as the following differential equation with respect to
the complex number $z(t)$ such as
\[
\dot{z}(t) = (\mu+ \omega i)z(t)-(1+bi)|z(t)|^2z(t) ,
\]
where $\mu$, $\omega$, and $b$ are real constants，
$i$ is the imaginary unit.
When the initial value are located at an arbitrary point in the complex plane, the trajectory of
the solution $z(t)$ converges to the limit cycle, which is the circular orbit with the radius $\sqrt{\mu}$
and the angular velocity $\omega-b\mu$.
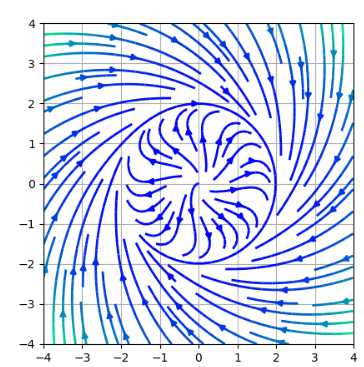
Coupled oscillator
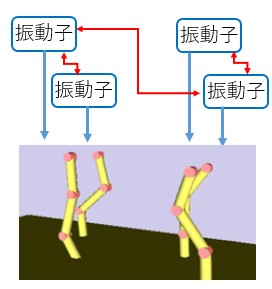
The phases of the periodical solutions of $n$ times of the Stuart-Landau equations
with respecto to the complex numbers $z_i(t)$ $(i=1, \cdots, n)$ are related to the
back-and-forth movements. Supposing that there exist mutual actions between the legs,
we define a gait generation model as a couple oscillator, which has coupled terms
expressing the mutual actions.
\[
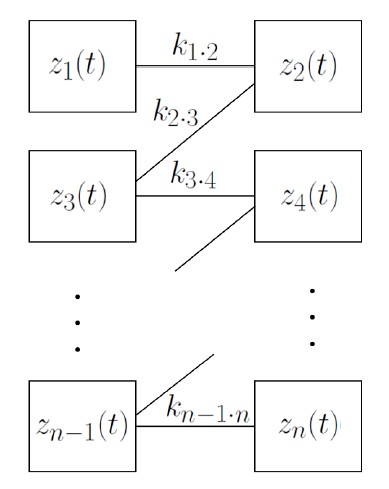\dot{z}_1(t) = (\mu_1 + \omega_1 i) z_1(t) - (1+b_1i)|z_1(t)|^2z_1(t) + k_{1\cdot2}(z_2(t)-z_1(t))
\]
\[
\dot{z}_2(t) = (\mu_2 + \omega_2 i) z_2(t) - (1+b_2i)|z_2(t)|^2z_2(t) + k_{1\cdot2}(z_1(t)-z_2(t))
+ k_{2\cdot3}(z_3(t)-z_2(t))
\]
\[
\vdots
\]
\[ \dot{z}_{n-1}(t) = (\mu_{n-1} + \omega_{n-1}i) z_{n-1}(t) - (1+b_{n-1}i)|z_{n-1}(t)|^2z_{n-1}(t)
+ k_{n-2\cdot n-1}(z_{n-2}(t)-z_{n-1}(t))
+ k_{n-1\cdot n}(z_n(t)-z_{n-1}(t))
\]
\[
\dot{z}_n(t) = (\mu_n + \omega_n i) z_n(t) - (1+b_ni)|z_n(t)|^2z_n(t) + k_{n-1\cdot n}(z_{n-1}(t)-z_n(t))
\]
where $\mu_i > 0$, $\omega_i$, $b_i$ $(i=1, \cdots, n)$ are real constants.
The paramemters $k_{1\cdot2}$, $k_{2\cdot3}$, $k_{3\cdot4}$, $\cdots$, $k_{n-1\cdot n}$ are real constants which mean
the coupling coefficients.
We assume that
\[
k_{i\cdot i+1} \neq 0, \ \ i=1, \cdots, n-1 \ .
\]
The variables $z_1$, $z_2$, $\cdots$, $ z_{n-1}$, and $z_n$ are related to the movoments of the legs,
the left leg at the first row, the right leg at the first row, $\cdots$, the left leg at the last row,
and the right leg at the last row.
Problem to be considered
There exist parameters $\mu_i$, $\omega_i$, $b_i$ $(i=1, \cdots, n)$ and $k_{i\cdot i+1}$ $(i=1, \cdots, n-1)$ in the
coupled oscillator.
For simplicity, the $\mu_i$ and $b_i$ $(i=1, \cdots, n)$ are set as $\mu_i=1$, $b_i=0$.
The problem in this research is clarifing how to determine the values of the parameters $\omega_i$ $(i=1, \cdots, n)$ and
$k_{i\cdot i+1}$ $(i=1, \cdots, n-1)$ in order to generate the given phase differences which are suitalbe for gait.
The parameters $\omega_i$ and $k_{i\cdot i+1}$ mean the natural frequency and the coupling coefficient, respectively.
The values of these parameters affect the behavior of each oscillator and the phase differences in the coupled oscillator.
Japanese version